Hva er variasjonsteori? En veiledning for primære matematikklærere (2024)

Denne bloggen vil se på konseptet Variasjonsteori og forsøke å avmystifisere det forvirrende språket rundt det. Håpet er at dette vil gjøre Variasjonsteori til et tilgjengelig og spennende verktøy som du kan begynne å bruke i mattetimene, eller gi deg en forståelse av hva som skjer dersom du kjenner igjen prinsippene, til tross for at du aldri har hørt om Variasjonsteori før!

Hvis du er premiummedlem av Third Space Learning, kan du få tilgang til en hel skoleCPD presentasjonsom dekker disse punktene i vår Maths Hub.

Hva er variasjonsteori i primær matematikk?

Variasjonsteori er en generell læringsteori som brukes overveiende i matematikkundervisning og pedagogikk. Det understreker et konsepts essensielle egenskaper ved å fokusere på hva som holdes ved like og hvilke endringer, noe som gir muligheten til å lage meningsfulle forbindelser.

Variasjonsteoriens opprinnelse

Studiet av variasjonsteori kommer hovedsakelig fra arbeid på tvers av to grupper av forskere som kom frem til lignende, men ikke helt samme konklusjoner.

Den ene var den svenske forskeren Ference Marton og kolleger som jobbet med konseptet Variation Theory; den andre var Gu Ling Yuan og teamet hans i Shanghai som kalte det Bianchi (undervisning med variasjon). Som man kunne forvente, har fremveksten av to lignende teorier skapt forvirring i enkelte områder av sektoren. I sammenheng med Storbritannia, skilles mellom dem sjelden, og derfor brukes aspekter av Bianchi under Variation Theory.

De er begge enige om at «den sentrale ideen med undervisning med variasjon er å fremheve de essensielle egenskapene til konseptene gjennom å variere de ikke-essensielle trekkene». (Gu, Huang & Marton, 2004). Denne bloggen vil hovedsakelig trekke på læringsstudiet til Gu og teamet hans.

Anvendelsen av variasjonsteori er mye bredere enn bare matematikkundervisningens domene, men snarere som en teori som underbygger hvordan elever lærer noe. Prinsippet som underbygger teorien er at ny læring skjer når de forstår hvordan et kritisk aspekt ved et nytt konsept endres (varierer) mot noe som ikke endres (invarians).

Ved å justere sin oppfatning av hva som har forblitt det samme og hva som har endret seg, er det mer sannsynlig at elevene lærer læringsobjektet og forstår de underliggende matematiske strukturene som studeres. Det er med andre ord når en pedagog nøye konstruerer spørsmål, vurderer rekkefølgen de vises i, og bringer tenkeprosessen mellom spørsmål på spissen for elevene, slik at det kan lages meningsfulle koblinger til de matematiske strukturene fra oppgaven.

Det er usannsynlig at et regneark i seg selv vil føre til den nødvendige kognitive prosessen hos elevene som trengs for å dra nytte av fordelene som Variasjonsteori gir elevene i deres konseptualisering av matematiske strukturer.

Ikke la deg lure til å kjøpe betalte ressurser som lover å få til variasjonsteori med bare et regneark, med mindre du spesifikt kan identifisere hvordan disse spørsmålene utfører prinsippene for læringsobjektet, og du føler deg trygg på at du kan få frem disse matematiske strukturene til elevene gjennom spørsmålet ditt på en veldig bevisst måte.

Faktisk, som du vil se gjennom noen eksempler, risikerer forsøk på variasjonsteori kun gjennom en regnearktilnærming og ingen dialog at elevene lærer mindre enn å ikke prøve å bruke variasjonsteorien.

Hva er typene variasjonsteori?

Det finnes to typer variasjonsteori; konseptuell variasjon og prosessuell variasjon.

Hva er prosessuell variasjon i matematikk?

Prosedyrevariasjon er en prosess for dannelse av matematiske ideer trinn for trinn, der elevenes erfaring med å løse problemer manifesteres av rikdommen av forskjellige problemer og variasjonen av overføringsstrategier.

Den er avledet fra tre deler:

1. Varierer problemet
2. Flere metoder for å løse et problem
3. Flere anvendelser av en metode på lignende problemer

Som med konseptuell variasjon, er nøkkelen til suksess å lære elevene å se etter sammenhenger innenfor de matematiske strukturene fra en tidlig alder.

Hva er konseptuell variasjon i matematikk?

Konseptuell variasjon er en prosess som ser på å gi elevene flere perspektiver og erfaringer innenfor et gitt konsept eller læringsobjekt. Det refererer til strategiene en lærer kan bruke for å bringe frem kritiske aspekter ved ønsket læringsutbytte, og øke deres forståelse ved å demonstrere det fra ulike perspektiver.

Marton og teamet hans av forskere konkluderte med at studenter merker forskjeller mellom ulike læringsobjekter før de legger merke til likhet.

Når du bruker konseptuell variasjonspedagogikk i klasseromsdiskurs, er det best å gi eksempler som er helt forskjellige før du ser på eksempler som er like. For eksempel, hvis du ønsker å demonstrere for elevene hva en trekant er, ville det være best å presentere en trekant sammen med andre former som ikke er trekanter for å hjelpe elevene å skille hva det er som lager en trekant.

Er dette en elefant?

En vanlig ikke-matematisk tilnærming for å forklare dette er å se på dyreriket.

Hvordan har det seg at vi er svært klar over hva en elefant er? Vi er i stand til å skille det ganske enkelt fra de utallige andre medlemmene av dyreriket. Hvis de blir presset for å svare på hvordan vi vet at bildet ovenfor er en elefant, er de to første funksjonene som folk beskriver for å forklare deres sikkerhet, snabelen og støttenner.

Svaret mitt er dette: er dette derfor IKKE en elefant?

Klart det er det. Men dette er en elefant uten brosme, og støttenner er et av kjennetegnene til en elefant som mange hevder. Kanskje vi kunne fortsette med å forklare at størrelsen på en elefant er et kjennetegn, eller den grå fargen. En elefant må være grå, ha snabel, være stor, og kan ha støttenner, men dette er ikke et krav.

Mitt svar er: hvis det er tilfelle, er dette en elefant?

Det er det åpenbart. Likevel er dette neppe et stort dyr og ville derfor ikke oppfylle vilkårene som stilles til det for å karakterisere det som en elefant ovenfra. Derfor kan en elefant være stor eller liten, ha støttenner eller ikke ha støttenner, være grå og ha snabel. De nødvendige betingelsene for hva som utgjør en elefant blir stadig klarere.

Vi vet også, instinktivt, at dette bildet ikke er en elefant til tross for at det er lite, grått og ikke har støttenner. Vi vet at det ikke kan være på grunn av ørene, formen på hodet og mangelen på stammen. Og her, gjennom vår visuelle oppfatning, kommer ideen om variasjonsteori til live.

Ved å se hva det er å være noe i så mange forskjellige former som mulig og i former som er relatert, enten det er nært eller på annen måte, er vi i stand til å se det konseptet fra flere perspektiver og erfaringer for å virkelig kjenne det. På sitt mest grunnleggende nivå er dette konseptuell variasjon.

Eksempler og ikke-eksempler på variasjonsteori

Som nevnt ovenfor, har vi en tendens til å gjenkjenne likhet før vi gjenkjenner forskjell. Det er fra dette prinsippet vi kan vurdere å introdusere kritiske aspekter ved matematiske strukturer gjennom eksempler og ikke-eksempler som vi deler med elevene. I dette tilfellet, for å forbli tro mot Martons funn, vil eksemplene som demonstrerer det kritiske læringsobjektet som vi vil at elevene skal lære være uforanderlige, men bakgrunnen vi underviser i vil variere. Deretter, når vi viser ikke-eksempler, handler de, som man kanskje kan forestille seg, for å definere hva det kritiske aspektet ikke er.

For eksempel, hvis du lærer betydningen av likhetstegnet, kan du ha eksempler på forskjellige beregninger som bruker alle fire operasjonene der svaret var riktig og eksempler som bruker alle de fire operasjonene der svarene var feil, og slik at ekvivalenstegnet ikke kunne brukes.

Standard og ikke-standard i variasjonsteori

Når studentene har utviklet en følelse av hva det kritiske aspektet er og ikke er, er det viktig å demonstrere dette aspektet i både standard og ikke-standard form.

Jeg husker første gang elevene jeg underviste kom over et regnestykke der likhetstegnet kom før noen sifre og andre symboler '__ = 8 + 9'. Det så forvirret ut som om de hadde fått i oppgave det umulige. Feilen med denne forvirringen var helt og holdent min egen, da hvert spørsmål jeg noen gang hadde stilt fokuserte på standardskjemaet når jeg skrev beregningen '8 + 9 =__'. Dette betydde at elevene ikke helt hadde skjønt symbolbegrepet og dets kritiske trekk; at det er der for å representere ekvivalens, ikke bare som et symbol som brukes til å skrive ned et svar i etterkant.

I undervisningssekvensen min for undervisningsekvivalens og likhetstegnet, etter å ha sett på eksempler og ikke-eksempler, burde jeg ha sett på standard- og ikke-standardformer som de nedenfor:

__ = 8 + 9

10 + 7 = 8 + 9

Denne grafikken kan være nyttig for å fremheve hvordan disse komponentene passer sammen.

Prosedyrevariasjon: hva er det samme, hva er annerledes og hva legger du merke til?

Vi kan bruke prosessuell variasjon til å fremheve mønstre innenfor et sett med spørsmål som bringer frem et kritisk læringspunkt eller læringsobjekt. La oss si at vi ønsket å trekke elevenes oppmerksomhet til en av feltaksiomene for multiplikasjon – distributivitet – slik at de kan bruke den når de vil når de skal håndtere enhver multiplikasjon. Vi kan presentere dette på følgende måte:

Den feilaktige måten å gå frem på vil være å behandle dette som et regneark, der du leverer et innspill og ber elevene ta knekken på og fullføre det. Det ville ikke være noen metode for den galskapen, og mulighetene for å få frem nye og tidligere lærte relasjoner mellom tallene ville sannsynligvis falle i veien for alle elever, eller ville bare bli funnet av de som er høypresterende i matematikk.

Snarere bør en mer kontrollert tilnærming tas. Du bør be elevene om å fullføre de to første spørsmålene og deretter spørre dem: «hva er likt, hva er annerledes og hva legger du merke til?» Dette vil gi muligheten til å fange opp hva utformingen av disse minimalt forskjellige spørsmålene forsøker. å trekke ut.

Prosedyrevariasjonstrinn

For det første vil du at elevene skal legge merke til forholdet mellom multiplikaden fra den gitte setningen (12) og kombinasjonen av multiplikadene fra de to første ligningene (11 + 1 og 10 + 2). Studentene vil bli trukket til det faktum at de alle utgjør det samme, og at produktet også kommer til å være 96.

Herfra kan elevene se om det stemmer for de neste to spørsmålene. Faren ved å la elevene fullføre alle 4 spørsmålene først uten å diskutere det, kan føre til at elevene ser at produktet er det samme, men ikke forstår forholdet mellom multiplikandene.

Legg merke til at 5^thspørsmålet i sekvensen opprettholder ikke det samme mønsteret nøyaktig. Multiplikantene er totalt 12, men multiplikatoren er nå halvparten av originalen. Dette er for å stoppe elevene målløst å skrive 96 ned uten å tenke over det.

Det er imidlertid avgjørende at utsagnet i begynnelsen fortsatt kan brukes til å løse dette, da svaret vil være halvparten av 96. Dette forholdet mellom multiplikatorene kan også trekkes frem. Spørsmål 6 lar den kommutative loven om multiplikasjon komme gjennom, så vel som den assosiative loven, og det siste spørsmålet forsterker divisjon som invers av multiplikasjon.

På alle punkter for å få elevene til å svare på disse spørsmålene i et kontrollert miljø, er spørsmålene "hva er likt, hva er forskjellig og hva legger du merke til?" de som brukes mest, slik at elevene kan ta hensyn til disse forskjellene og likhetene. . Faktisk kan det å fullføre øvelsen ovenfor ta det aller meste av leksjonen, og elevene vil få mer ut av å fullføre den enn et helt regneark.

Problemløsning i prosedyrevariasjon

I hjertet av prosedyrevariasjon er tre former for problemløsning:

1. Variere et problem – utvide det opprinnelige problemet ved å variere betingelsene, endre resultatene og generalisere;
2. Bruken av flere metoder for å løse et problem ved å variere de ulike prosessene for å løse et problem og assosiere ulike metoder for å løse et problem;
3. Flere anvendelser av en metode ved å bruke samme metode på en gruppe med lignende problemer.

1. Prosedyrevariasjon: variere problemet

Denne formen for variasjon tar sikte på å konsolidere et konsept ved å variere visse forhold for å bringe informasjon, ofte informasjon som er i konflikt med elevenes nåværende forståelse av konseptet, frem i lyset. Se på eksemplet nedenfor:

Variasjonen innenfor disse problemene bør være innlysende. Mengden eplejuice forblir konstant, og bare mengden som hver krukke inneholder varierer spørsmål for spørsmål. Elever er ofte komfortable med deling som å dele i like grupper (spesielt på barneskolen), der elevene kan generalisere at deling resulterer i å gjøre noe mindre.

Det er denne misforståelsen som eksemplet ovenfor forsøker å utnytte gjennom de tre siste spørsmålene. Vi ser faktisk at å dele med et helt tall og desimal gir en kvotient som er større enn utbyttet.

2. Prosedyrevariasjon: variere metoden

Denne typen variasjoner er en som mange lærere gjør, men kanskje ikke er klar over. Bare å undervise og demonstrere ulike metoder for å løse et problem er det første trinnet i denne typen variasjon, men suksessen ligger i å kunne trekke frem det elevene legger merke til om likhetene og forskjellene mellom hver representasjon. Her er noen få utførte eksempler for å variere metoden for å løse 12 × 5.

Skolens beregningspolicy bør angi hvilke metoder som vil bli introdusert og når. White Rose Maths har laget en beregningspolicy som ser på hvilke ulike metoder som kan læres. Atdokumenter tilgjengelig fra TES gratis.

3. Prosedyrevariasjon: multippel anvendelse av en metode på lignende problemer

Dette siste eksemplet ser på å få til variasjon, ikke gjennom å endre metoden, men ved å bruke en metode eller representasjon mot en gruppe varierte, men like problemer.

Variasjonsteori eksempler KS1

I KS1 kan dette se slik ut:

1) James har 8 blomster og Julie har 5 blomster. Hvor mange blomster er det til sammen?
2) James har 5 blomster og Julie har 8 blomster. Hvor mange blomster er det til sammen?
3) Det er 13 blomster, noen er røde og noen er blå. 8 er røde. Hvor mange er blå?
4) Det er 13 blomster, noen er røde og noen er blå. 8 er blå. Hvor mange er røde?

Her er problemene varierte, men plassert i en lignende kontekst, og tallene som brukes er de samme, men hva hvert spørsmål ber elevene om å gjøre, er litt forskjellig. For eksempel, for spørsmål én, kan elevene bruke Cuisenaire-stenger for å visualisere problemet. De la ned den gule stangen og den brune stangen for å lage et tog og deretter den oransje og den grønne over (eller under) for å hjelpe til med å løse totalen.

Spørsmål to lar elevene eksperimentere med den kommutative loven om addisjon. Legg merke til hvordan alle stengene som brukes er like, men rekkefølgen som bunntoget er konstruert i har endret seg. Den underliggende strukturen forblir uendret.

Spørsmål tre forteller oss at det er tretten blomster til sammen og 8 av dem er røde. Det neste trinnet vil være å se hvor mange flere som trengs for å ta 8 opp til 13. Elevene kan i utgangspunktet bruke hvite stenger før de bytter den ut mot en gul stav av samme verdi. Igjen forblir den underliggende strukturen til problemet uendret.

Det siste spørsmålet er bare det motsatte av spørsmål 3. Vi vet den totale mengden blomster og at en viss delmengde av dem er lik 5. Derfor, for å finne den manglende mengden, må vi telle opp fra 5 til vi kommer til 13. Igjen. , elevene må kanskje bruke 8 hvite stenger først, men de vil se at denne kan byttes ut med en brun stang.

Ved slu*tten av denne øvelsen vil elevene kunne se at de 4 spørsmålene har lignende underliggende strukturer til tross for variasjonen innenfor oppgavene.

Variasjonsteori fungerte eksempler

Som nevnt ovenfor, vil ikke bare det å gi studentene spørsmål som inneholder aspekter av variasjonsteorien bringe fordelene med tilnærmingen. Derfor, hvis du ikke forstår variasjonen som finner sted, ville det sannsynligvis være best å ikke bruke disse eksemplene.

For hver av disse trenger vi mange eksempler på hvordan varianten du referer til ser ut "i praksis". Med andre ord, med referanse til vanlige slags spørsmål og læringsmål fra den nasjonale læreplanen, slik at lærere kan lese den og se hvordan de kan prøve å implementere den i sin egen leksjon.

Hvis du kan trekke fra hvert av hovedemnene i den nasjonale læreplanen, ville det vært flott, men det er egentlig bare et tilfelle av å vise det store utvalget av måter folk kan tenke på å inkludere denne praksisen i undervisningen.

Talleksempler: tall og stedsverdi

Eksemplene nedenfor varierer representasjonene for å gi tilgang til den samme ideen. Denne tilnærmingen kan enkelt overføres på tvers av alle årskull for å se på plassverdimål. Å bruke dette i en KS1-klasse vil innebære å se på hver representasjon og veilede elevene gjennom prosessen med å spørre «hva er likt, hva er forskjellig, og hva legger du merke til?» Å introdusere elevene for disse spørsmålene tidlig vil forhåpentligvis resultere i dem blir internalisert automatisk, og derfor vil elevene naturlig stille seg selv disse spørsmålene.

Bruken av farge er spesielt nyttig her ettersom den støtter forbindelser mellom plassverditellerne, kort og base 10, men tilstedeværelsen av Cuisenaire-stangen ogNumicon(hvis farger ikke samsvarer med dette) stopper assosiasjonen av "tiere" som er grønne osv.

Et avgjørende element å trekke ut av studentene er foreningen av 2 i noen representasjoner, eller hvor 2 har blitt bevart som 2 enere. Tallnettet gir en mulighet til å koble disse representasjonene innenfor det abstrakte tallsystemet.

Talleksempler: addisjon og subtraksjon

563 – 100 = ___ – 200

387 – 100 = ___ – 200

983 – 100 = ___ – 200

___ – 100 = 874 – 200

Dette spørsmålet fokuserer på å subtrahere med multipler av 100 og elevenes forståelse av likhetstegnet. Det er subtrahenden som forblir invariant mens minuenden varierer. Dette gjøres slik at generaliseringer kan frembringes med hensyn til subtraksjon av multipler av 100. Minuendene i seg selv spiller ingen stor rolle i å få til effektene av variasjonsteori.

Her vil vi at elevene skal forstå at «lik» ikke betyr «svar», men at to matematiske utsagn er balansert og produserer et produkt som er det samme som hverandre.

Vi kan også få til forholdet mellom de to minuendene, hvorav den ene er ukjent, sammenlignet med effekten av å subtrahere den første med hundre. Nemlig at tiere og enere ikke endres og at etter hvert som subtrahenden har økt med 100 fra 100 til 200. For at proporsjonaliteten skal holde seg konstant mellom hvert utsagn, må minuenden også øke med 100.

Det vil være i elevenes interesse å raskt trekke et multiplum av 100 fra et 4-sifret tall der forskjellen er et 3-sifret tall i påfølgende leksjoner, slik at de kan se hvilken innvirkning dette kan ha på generaliseringene de produserer.

Talleksempler: multiplikasjon og divisjon

Hva er likt/forskjellig og hva legger du merke til?

__ × 5 =__

5 × __ =__

__ =__ × __

__ + __ + __ + __ + __ = __

__ × 7 =__

7 × __ = __

__ =__ × __

__ + __ + __ + __ + __ + __ + __ = __

Skriv det du legger merke til nedenfor.

Denne oppgaven knytter multiplikasjon til array-/arealmodellen for multiplikasjon, forståelsen av likhetstegnet, den kommutative loven for multiplikasjon og multiplikasjon som gjentatt addisjon.

Elevene vil gjenkjenne at svaret er 35 og at de i den første modellen kan se 7 grupper på 5 når de ser vertikalt på tvers fra venstre til høyre. Når du ser på det horisontalt fra topp til bunn, kan 5 grupper på 7 sees. De kan bruke disse faktaene til å skrive en multiplikasjonsberegning der produktet skrives først for å få til deres forståelse av likhetstegnet, og relatere multiplikasjonen av hver vertikal kolonne til gjentatt addisjon av antall kolonner totalt.

Det motsatte er tilfellet med den andre representasjonen der det er 5 grupper på 7 på horisontalen og 7 grupper på 5. Slike aktiviteter vil hjelpe elevene til å forstå forskjellen i visuell representasjon når de samme tallene brukes som multiplikant og multiplikator på tvers. to forskjellige beregninger.

Talleksempler: brøker, forholdstall og proporsjoner

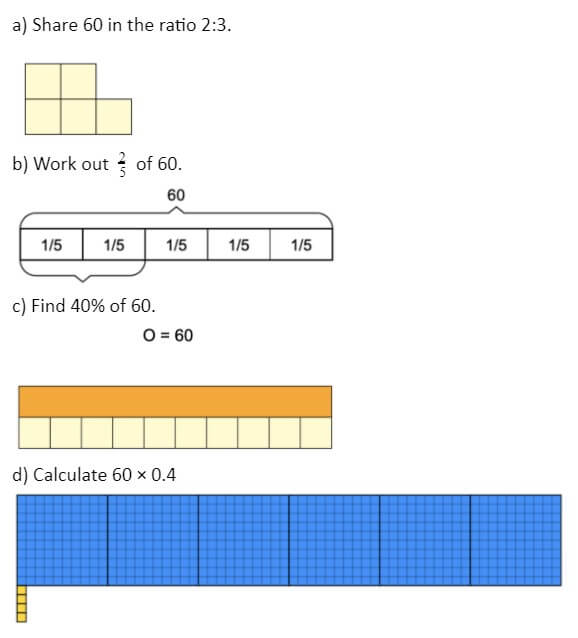
Denne serien med spørsmål er utformet for å koble sammen alle de ovennevnte områdene med brøk og forhold. Dette er viktig ettersom sammenhengene mellom prosenter og forhold kan gå glipp av, og derfor brukes mer tid enn nødvendig for å lære begrepet forholdstall.

Her varierer metodene som brukes, men spørsmålet er nøyaktig det samme, om enn i sammenheng med konseptet det trekker frem. Som sådan vil svaret være nøyaktig det samme for hvert spørsmål (24), men metodene og den matematiske tenkningen bak hver tilnærming vil trekke frem sammenhengen mellom spørsmålet, samt de forskjellige representasjonene som har blitt brukt, for eksempel telleren og nevner av en brøk. Legg merke til hvordan alt det ovennevnte enten er konkret eller billedlig.

Måleeksempler

Følgende oppgave kommer fra @J0shMartin og hans bidrag til Craig Bartons nettsted for Variation Theory. Selv om dette overveiende er en sekundærbasert nettside, er det noen eksempler som er relevante for KS2. Følgende oppgave krever at elevene legger merke til mønstre når de konverterer mellom målinger (noe elevene bør ha en viss forståelse for å gjøreFØRde tar fatt på denne oppgaven).

Svarene er gitt nedenfor:

1. 3 m
2. 0,3 m
3. 0,3 m
4. 0,03 m
5. 4500 mm
6. 450 cm
7. 45 cm
8. 5 cm
9. 50 mm
10. 15 000 m
11. 1500 m
12. 100 m
13. 50 m

Siden dette er en kontekst som mange lærere kjenner til, her vil det være best for deg å prøve å vurdere hvordan spørsmålene er nøye utformet for å få til variasjon, og hvordan du kan gå frem for å bruke denne sekvensen i din egen leksjon. Vurder spørsmålene du vil stille, antall spørsmål du vil få elevene til å svare på før du stopper dem for å diskutere oppgaven så langt, og hvordan du vil forklare mønstrene for elevene.

Eksempler på geometri: egenskaper til former

Formegenskap er et spesielt nyttig læreplanområde for å distribuere Variasjonsteori og kan brukes fra år 1 og utover med stor effekt. Nedenfor er en sekvens av lysbilder brukt i en leksjon om å beskrive rektangler med noen elever i 1. klasse.

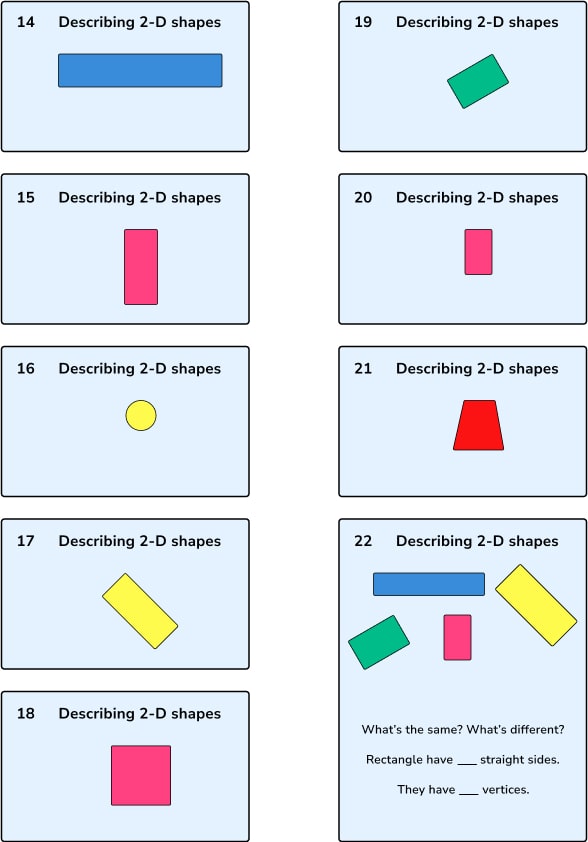
Rotasjonen, fargen og typen form har alle variert slik at elevene kan generalisere om egenskapene til rektangler (mange mente at de på lysbilde 17 og 19 ikke var det), slik at de virkelig kan se formens kjennetegn og ikke bli fanget på elementer som ikke er viktige.

Dette er den konseptuelle variasjonen som skissert i starten av denne bloggen i aksjon. Den bruker eksempler og ikke-eksempler, standard- og ikke-standardeksempler for å trekke frem hva det betyr at en form er et rektangel.

Vanlige spørsmål om variasjonsteori

Likte dette? Hvorfor ikke prøve vår 'How I Wish I'd I'd Taught Maths'-serie, inspirert av Craig Bartons bestselgende bok:

• Kognitiv belastningsteori(1)
• Direkte instruksjon og Rosenshine-prinsipper for instruksjon(2)
• Målfrie problemer og fokusert tenkning(3)
• Bevisst praksis i utdanning(4)
• Kritisk tenkning og problemløsningsaktiviteter KS2(5)
• Hvordan gjenfinningspraksis hjelper langsiktige matematikkferdigheter(6)
• I tillegg til:Mest effektive undervisningsstrategier

Nettbaserte 1-til-1 mattetimer som er tiltrodd av skoler og lærere
Hver uke støtter Third Space Learnings matteveiledere tusenvis av barneskolebarn med ukentlige online 1-til-1 leksjoner ogmatematiske intervensjoner. Siden 2013 har vi hjulpet over 150 000 barn til å bli tryggere og dyktigere matematikere.Lære merellerbe om et personlig tilbudfor å snakke med oss ​​om dine behov og hvordan vi kan hjelpe.